Harry Potter
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
| Berkas:Potterindo.jpg Sampul buku pertama seri Harry Potter, Harry Potter dan Batu Bertuah versi bahasa Indonesia | |
| Penulis | J. K. Rowling |
|---|---|
| Negara | Inggris |
| Bahasa | Inggris |
| Genre | Fantasi |
| Penerbit | • Bloomsbury Publishing (Inggris) • Scholastic Corporation (AS) • Gramedia Pustaka Utama (Indonesia) • dan lain-lain di berbagai negara. |
| Tanggal terbit | September 2000 |
| Terbitan dalam Bahasa Inggris | 26 Juni 1997 (UK) 1 September 1998 (Amerika Serikat) |
Latar belakang kisah ini kebanyakan berada di Sekolah Sihir Hogwarts dan berpusat pada pertarungan Harry Potter melawan penyihir jahat Lord Voldemort, yang menggunakan Ilmu Hitam untuk membunuh orang tua Harry.
Kesemua tujuh buku yang direncanakan Rowling dalam seri novel ini telah diterbitkan. Buku keenam, Harry Potter dan Pangeran Berdarah-Campuran versi asli bahasa Inggris diterbitkan pada 16 Juli 2005, sementara buku ketujuh, Harry Potter dan Relikui Kematian diluncurkan di seluruh dunia pada 21 Juli 2007 (versi terjemahan bahasa Indonesia diterbitkan pada tanggal 13 Januari 2008). Enam buku pertama dalam seri novel ini secara keseluruhan telah terjual lebih dari 325 juta kopi, dan telah diterjemahkan ke lebih dari 63 bahasa.[1][2]
Atas kesuksesan novel-novelnya ini, Rowling telah menjadi penulis terkaya sepanjang sejarah kesusasteraan.[3] Versi-versi asli dalam bahasa Inggris diterbitkan oleh penerbit Bloomsbury di Inggris Raya, Scholastic Press di Amerika Serikat, Allen & Unwin di Australia, dan Raincoast Books di Kanada. Versi bahasa Indonesia diterbitkan oleh Gramedia Pustaka Utama.
Lima buku pertama telah diangkat menjadi film layar lebar oleh Warner Bros. dan mendulang kesuksesan besar. Film kelima, Harry Potter and the Order of the Phoenix, mulai diambil gambarnya pada Februari 2006, dan dirilis pada 11 Juli 2007 di Amerika Serikat. Film keenam, Harry Potter and Half Blood Prince, dirilis pada 15 Juli 2009.[4]
Daftar isi[sembunyikan] |
[sunting] Tentang penciptaan Harry Potter
Ide tentang Harry Potter pertama kali tercetus dalam pikiran J. K. Rowling ketika menaiki kereta api dari Manchester ke London pada tahun 1990. Pada waktu itu, dia baru saja bercerai dan mengambil inisiatif untuk menjadikan Harry Potter sebagai inspirasi hidupnya. Dia menghabiskan waktu di dalam perjalanannya itu dengan memikirkan plot yang lengkap tentang ceritanya itu. Di situs webnya, Rowling menceritakan pengalamannya itu:| “ | Saya telah menulis hampir tanpa jeda sejak umur enam tapi sebelumnya saya tidak pernah merasa begitu bergairah akan suatu gagasan. Saya hanya duduk dan berpikir, selama empat jam (menunggu keterlambatan kereta api), dan semua detel bermunculan di otak saya, dan anak laki-laki ceking berambut hitam dan berkaca mata yang tidak menyadari bahwa ia adalah seorang penyihir menjadi semakin lama semakin nyata bagi saya. | ” |
Walaupun Rowling menyatakan bahwa ia tidak memiliki target khusus mengenai umur pembacanya ketika ia mulai menulis buku-buku Harry Potter, penerbitnya pada permulaannya telah menetapkan target pembacanya antara umur sembilan hingga sebelas.[6] Pada malam sebelum penerbitan, Joanne Rowling diminta oleh penerbitnya untuk menggunakan nama samaran yang lebih netral-jender, supaya dapat menarik anak laki-laki dalam jangkauan umur tersebut, karena mereka khawatir bahwa anak laki-laki tidak akan tertarik membaca novel yang mereka ketahui ditulis oleh seorang wanita. Ia memilih untuk menggunakan nama J. K. Rowling (Joanne Kathleen Rowling), mengambil nama neneknya sebagai nama keduanya, karena ia tidak memiliki nama tengah.[7]
Buku pertama Harry Potter diterbitkan di Britania Raya oleh Bloomsbury pada Juli 1997. Di Amerika Serikat buku ini diterbitkan oleh Scholastic pada September 1998, di mana Rowling menerima $105.000 untuk hak penerbitan Amerika Serikat — sebuah nilai yang tidak biasa bagi sebuah buku anak-anak yang dikarang oleh pengarang yang tidak dikenal (pada saat itu).[8] Khawatir bahwa para pembaca di Amerika tidak mengerti kata "philosoper" atau tidak menganggapnya sebagai tema magis (karena "Philosoper's Stone" atau batu filsuf adalah kata dalam bidang alkimia), Scholastic bersikeras untuk mengganti nama buku itu menjadi Harry Potter and the Sorcerer's Stone untuk pasar Amerika.
Selama hampir satu dasawarsa, Harry Potter telah mengalami kesuksesan besar, tidak hanya karena resensi yang positif dan strategi pemasaran penerbit Rowling, tetapi juga karena pembicaraan dari mulut ke mulut di antara para penggemarnya, terutama di antara para remaja laki-laki. Kalangan remaja laki-laki ini menjadi penting, karena selama bertahun-tahun kalangan ini semakin tidak tertarik dengan bacaan yang dianggap ketinggalan zaman ketimbang video game dan internet. Penerbit Rowling berhasil menangkap kegairahan di kalangan remaja laki-laki ini dan segera merilis keempat buku pertama berturut-turut secara cepat, sehingga kegairahan mereka tidak sempat meredup ketika Rowling bermaksud untuk istirahat menulis di antara rilis Harry Potter dan Piala Api dan Harry Potter dan Orde Phoenix, dan dengan segera terbentuklah grup pembaca yang loyal.[9] Seri ini juga mendapatkan para penggemar dewasa, dengan diterbitkannya dua edisi untuk setiap buku Harry Potter (di Kanada dan Britania Raya, tapi tidak di Amerika Serikat). Keduanya memiliki naskah yang sama persis, tetapi dengan sampul yang berbeda, untuk masing-masing edisi anak-anak dan dewasa.[10]
[sunting] Kisah
[sunting] Ringkasan plot
- Untuk sinopsis per novel, lihat artikel yang relevan di masing-masing seri.
Pada malam berikutnya, seorang penyihir membawa Harry ke rumah Bibi dan Pamannya, Dursley, tempat di mana ia akan tinggal bertahun-tahun setelahnya. Keluarga Dursley adalah famili Harry yang kejam dan merupakan orang-orang non-penyihir. Mereka senantiasa berusaha menyembunyikan latar belakang Harry yang merupakan penyihir dan keturunan penyihir, dan memberinya hukuman jika terjadi kejadian-kejadian aneh.
Pada ulang tahunnya yang kesebelas, Harry mendapatkan kontak pertamanya dengan dunia sihir, ketika ia menerima surat dari Sekolah Sihir Hogwarts, yang berusaha disembunyikan oleh Paman dan Bibinya, hingga ia tidak berhasil membaca surat tersebut. Surat itu pada akhirnya dapat dibacanya setelah ia ditemui oleh Hagrid, Pengawas Binatang Liar di Hogwarts. Hagrid memberitahunya bahwa ia sesungguhnya adalah seorang penyihir, dan surat itu memberitahunya bahwa ia disediakan tempat untuk belajar di Hogwarts. Setiap jilid dari novel Harry Potter mengisahkan mengenai satu tahun kehidupan Harry, yang kebanyakan dihabiskannya dalam pelajaran di Hogwarts, di mana ia mempelajari penggunaan sihir dan membuat ramuan. Harry juga mempelajari bagaimana mengatasi rintangan-rintangan sihir, sosial, dan emosi selama masa remajanya. Dalam periode yang sama, Voldemort juga berusaha untuk kembali ke tubuh fisiknya dan mengembalikan seluruh kekuatannya, sementara Kementrian Sihir berusaha juga untuk menolak untuk mengakui adanya ancaman akan kembalinya Voldemort. Penolakan Kementerian Sihir ini kemudian menyebabkan banyak kesulitan bagi Harry Potter.
[sunting] Dunia Harry Potter
Dunia sihir dalam kisah Harry Potter adalah dunia yang ada di dunia kita sekarang tapi juga sekaligus terpisah sama sekali secara sihir. Kalau diperbandingkan, dalam kisah fantasi Narnia dunia sihirnya merupakan dunia alternatif, sementara dalam Lord of the Rings Bumi-Tengah merupakan dunia mite pada masa lampau. Lingkungan sihir Harry Potter dikisahkan berada di tengah-tengah dunia kita saat ini, dengan benda-benda sihir yang mirip dengan benda-benda di lingkup non-sihir. Lembaga-lembaga dan lokasi-lokasinya pun mirip atau malah sama dengan yang berada di dunia nyata, seperti London. Lingkungan sihir sama sekali tidak dapat terlihat oleh populasi non-sihir (atau Muggle, misalnya: Keluarga Dursley).Bakat sihir adalah kemampuan alami yang telah ada sejak lahir, tidak dapat muncul karena dipelajari. Mereka yang memiliki bakat sihir harus mengikuti pelajaran di sekolah-sekolah seperti Hogwarts untuk dapat menguasai dan mengontrolnya. Namun demikian, ada kemungkinan anak-anak yang lahir di keluarga penyihir yang hanya memiliki sedikit bakat sihir atau malah tidak ada sama sekali (disebut "Squibs", misalnya Mrs. Figg, Argus Filch). Para penyihir belum tentu dilahirkan dalam keluarga penyihir, dan banyak dari mereka yang dilahirkan dari orang tua (para Muggle) yang sama sekali tidak mengenal sihir. Mereka yang murni berdarah penyihir seringkali tidak terbiasa dengan dunia Muggle, malah terasa lebih aneh bagi mereka ketimbang kita memandang dunia mereka. Namun demikian, dunia sihir dan elemen-elemennya yang menakjubkan itu digambarkan sebagai dunia-yang-sangat-mirip-dengan-dunia-nyata. Salah satu tema utama dalam novel ini adalah keberadaan dunia sihir dan dunia biasa; di mana para tokohnya hidup dalam lingkungan yang memiliki masalah-masalah yang "normal", sekalipun mereka hidup di antara sihir.
[sunting] Hal-hal yang berulang
- Kemurnian darah (Harry Potter):
- Para penyihir pada umumnya memandang Muggle dengan sikap merendahkan dan curiga, masalahnya, sikap ini menjadi kefanatikan bagi sebagian kecil penyihir. Mereka yang fanatik ini mengkotak-kotakkan diri mereka atas dasar banyaknya leluhur mereka, di mana penyihir "berdarah-murni" (mereka yang keluarganya seluruhnya adalah penyihir) dianggap sebagai yang paling tinggi, penyihir "berdarah-campuran" (mereka yang memiliki keturunan penyihir dan Muggle) pada tingkat menengah, dan "kelahiran-Muggle" (mereka yang tanpa keturunan penyihir) sebagai yang terendah. Para pendukung kemurnian-darah percaya bahwa hanya mereka yang "berdarah-murni"-lah yang berhak mengontrol dunia sihir, dan tidak menganggap bahwa penyihir "kelahiran-Muggle" sebagai penyihir yang sesungguhnya. Beberapa dari mereka bahkan bertindak terlalu jauh dengan membunuhi para "kelahiran-Muggle" supaya jangan dapat mempelajari sihir. Kebanyakan kaum fanatik ini adalah berdarah-murni, sekalipun perlu dicatat bahwa Voldemort, yang mendukung fanatisme ini, sesungguhnya adalah penyihir berdarah-campuran. Selain itu, sebenarnya hanya tinggal sedikit sekali penyihir yang benar-benar berdarah-murni, oleh karena tanpa menikah dengan populasi Muggle, para penyihir lama kelamaan akan habis. Namun demikian, banyak keluarga penyihir yang menutupi bahwa ada di antara keluarga mereka yang menikahi kaum Muggle. Salah satu contoh keluarga seperti ini adalah dalam keluarga Black.[HP5]
- Burung hantu
[sunting] Karakter
[sunting] Struktur dan genre
[sunting] Tema dan motif
[sunting] Kritik dan pujian
[sunting] Kontroversi
[sunting] Publikasi Buku The Half-Blood Prince sebelum tanggal peluncuran
Publikasi besar-besaran Half-Blood Prince diwarnai dengan kontroversi yang tak terelakkan dan tidak terduga sebelumnya. Pada Mei 2005, para petaruh di Inggris menangguhkan taruhan mengenai tokoh utama mana yang akan tewas dalam buku tersebut karena kekhawatiran akan adanya petaruh dengan pengetahuan orang-dalam. Sejumlah taruhan besar dibuat untuk kematian Albus Dumbledore, kebanyakan berasal dari Bungay, Suffolk, tempat di mana buku-buku tersebut dicetak. Pertaruhan kemudian dibuka kembali. Kontroversi lainnya termasuk "hak membaca" buku-buku Potter yang tidak sengaja terjual sebelum tanggal peluncurannya, masalah lingkungan mengenai sumber dari kertas yang dipergunakna untuk mencetak jutaan buku tersebut, dan reaksi penggemar terhadap perkembangan plot dan pengungkapan dalam novel tersebut.Pada awal Juli 2005, Real Canadian Superstore, sebuah toko retail besar di Coquitlam, British Columbia, Kanada, secara tidak sengaja menjual empat belas buku The Half-Blood Prince sebelum tanggal peluncuran yang resmi. Penerbit Kanada, Raincoast Books, mendapatkan perintah keras dari Mahkamah Agung British Columbia untuk melarang pembelinya membaca buku-buku tersebut sebelum tanggal rilis resmi dan melarang mereka untuk membicarakan isinya.
Para pembeli tersebut ditawari sebuah kaus Harry Potter dan buku yang telah ditandatangani penulisnya jika mereka mengembalikan buku-buku itu sebelum 16 Juli 2005.
Pada 15 Juli 2005, kurang dari 12 jam sebelum buku ini resmi diluncurkan, Raincoast memperingatkan koran The Globe and Mail yang mempublikasikan sebuah resensi dari seorang penulis Kanada pada tengah malam, sebagaimana dijanjikan koran tersebut, sebagai pelanggaran atas perintah pengadilan akan kerahasiaan perdagangan. Perintah pengadilan ini dengan segera menjadi berita di berbagai artikel berita yang menyatakan bahwa perintah itu telah melanggar hak-hak asasi. Seorang guru besar hukum Kanada, Michael Geist mengomentari masalah ini dalam weblognya.[rujukan?] Richard Stallman, seorang aktivis lingkungan dan pendiri GPL menyerukan pemboikotan, dan meminta penerbitnya untuk meminta maaf. The Globe and Mail mempublikasikan resensi dari dua orang penulis dari Inggris pada edisi 16 Juli, dan mempublikasikan resensi dari penulis asal Kanada tadi pada situs web mereka pada pukul 9 pagi. Penjelasan juga tersedia di situs web Raincoast.
Selain kontroversi tersebut di atas, pada minggu yang sama, sebuah toko swalayan Chicago, Walgreens, secara tidak sengaja[rujukan?] juga menjual sebuah buku tersebut. Ketika si pembeli membaca mengenai insiden di Kanada di Internet, pembeli ini menyatakan bahwa ia tidak akan mengembalikan buku tersebut, tapi ia tidak akan membaca novel tersebut hingga tanggal rilis Amerika Serikat.
[sunting] Kontroversi Lingkungan Hidup
Buku Harry Potter ini juga membuat kontroversi pada masalah lingkungan hidup. Sebelum dan sesudah peluncuran buku tersebut, organisasi lingkungan Greenpeace dan National Wildlife Federation, mendorong konsumen di Amerika Serikat yang berencana membeli Harry Potter and the Half-Blood Prince untuk membelinya dari terbitan Kanada, Raincoast Books, yang mencetaknya di atas kertas daur ulang 2%, bebas-klorin, dan tidak menggunakan bahan dari pepohonan purba. Edisi Amerika Serikat pada buku tersebut, yang diterbitkan oleh Scholastic Press, dicetak di atas kertas yang tidak diketahui kadar persentase daur ulangnya, karena Scholastic menolak untuk mengumumkannya kepada publik. Namun Scholastic mengklaim di halaman terakhir buku tersebut, bahwa buku itu tidak menggunakan serat kayu dari pepohonan purba.[sunting] Film-film
[sunting] Penghargaan
[sunting] Kesuksesan komersial
Seri film Harry Potter adalah sebuah seri film fantasi berdasarkan novel Harry Potter karya seorang penulis berkebangsaan Inggris, J. K. Rowling. Film ini merupakan salah satu film dengan keuntungan kotor terbesar sepanjang masa senilai $3,5 miliar, di bawah serial-serial James Bond ($4,3 miliar) dan Star Wars ($6 miliar). Namun demikian, seri Harry Potter merupakan film dengan keuntungan kotor terbesar di dunia untuk kategori film yang diadaptasi dari buku, dan mengalahkan trilogi film The Lord of the Rings ($2,9 miliar)[rujukan?][sunting] Pengaruh terhadap kebudayaan
[sunting] Pengaruh terhadap kebudayaan pop
[sunting] Kelanjutan
Pada saat ini masih ada dua film Harry Potter yang akan dirilis. Film keenam, Half-Blood Prince sudah dirilis pada Juli 2009 dan film ketujuh, the Deathly Hallows.[sunting] Seri-seri Harry Potter
- Harry Potter and the Sorcerer's Stone (Harry Potter and the Philosopher's Stone di negara lain selain U.S)
- Penayangan perdana: 16 November 2001
- Sutradara: Chris Columbus
- Harry Potter and the Chamber of Secrets
- Penayangan perdana: 15 November 2002
- Sutradara: Chris Columbus
- Harry Potter and the Prisoner of Azkaban
- Penayangan perdana: UK: 31 Mei, USA: 4 Jun 2005
- Sutradara: Alfonso Cuarón
- Harry Potter and the Goblet of Fire
- Penayangan perdana: 2005, Filipina dan Indonesia: 16 November; Singapura, Malaysia, Swedia : 17 November; Britania Raya, Amerika Serikat, dan negara lain: 18 November 18; Australia: 1 Desember; Rusia: 23 Desember, Rusia merupakan negara paling akhir yang menayangkannya.
- sutradara: Mike Newell
- Harry Potter and the Order of the Phoenix
- Penayangan perdana: 13 Juli 2007
- Sutradara: David Yates
- Harry Potter and the Half-Blood Prince
- Penayangan perdana: Diperkirakan tahun 2009 (Juli)
- Sutradara: David Yates
- Harry Potter and the Deathly Hallows
- Mula ditayangkan: 2010
- Sutradara: Belum diketahui
[sunting] Buku terkait
- Hewan-hewan Fantastis dan Di Mana Mereka Bisa Ditemukan (Inggris-2001, Indonesia-2002)
- Quidditch dari Masa ke Masa (Inggris-2001, Indonesia-2002)









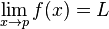
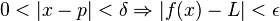

 ,
,
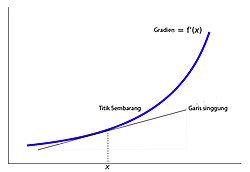
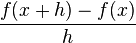 pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.
pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x. Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut.

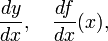 ataupun
ataupun 
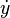 mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang
mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang 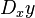 atau
atau 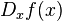 .
.

 , seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).
, seperti huruf S yang memanjang (S singkatan dari "Sum" yang berarti penjumlahan).

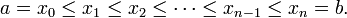
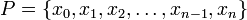 tersebut kita sebut sebagai partisi [a,b], yang membagi [a,b] menjadi sejumlah n subinterval
tersebut kita sebut sebagai partisi [a,b], yang membagi [a,b] menjadi sejumlah n subinterval ![[x_0, x_1], [x_1,x_2], \ldots, [x_{n-1}, x_n]](http://upload.wikimedia.org/math/7/9/b/79beb5191713ec5bd330992f316899ed.png) . Lebar subinterval pertama [x0,x1] kita nyatakan sebagai Δx1, demikian pula lebar subinterval ke-i kita nyatakan sebagai Δxi = xi - xi - 1. Pada tiap-tiap subinterval inilah kita pilih suatu titik sembarang dan pada subinterval ke-i tersebut kita memilih titik sembarang ti. Maka pada tiap-tiap subinterval akan terdapat batangan persegi panjang yang lebarnya sebesar Δx dan tingginya berawal dari sumbu x sampai menyentuh titik (ti, ƒ(ti)) pada kurva. Apabila kita menghitung luas tiap-tiap batangan tersebut dengan mengalikan ƒ(ti)· Δxi dan menjumlahkan keseluruhan luas daerah batangan tersebut, kita akan dapatkan:
. Lebar subinterval pertama [x0,x1] kita nyatakan sebagai Δx1, demikian pula lebar subinterval ke-i kita nyatakan sebagai Δxi = xi - xi - 1. Pada tiap-tiap subinterval inilah kita pilih suatu titik sembarang dan pada subinterval ke-i tersebut kita memilih titik sembarang ti. Maka pada tiap-tiap subinterval akan terdapat batangan persegi panjang yang lebarnya sebesar Δx dan tingginya berawal dari sumbu x sampai menyentuh titik (ti, ƒ(ti)) pada kurva. Apabila kita menghitung luas tiap-tiap batangan tersebut dengan mengalikan ƒ(ti)· Δxi dan menjumlahkan keseluruhan luas daerah batangan tersebut, kita akan dapatkan: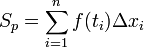
 mendekati nol, maka kita akan mendapatkan luas daerah tersebut.
mendekati nol, maka kita akan mendapatkan luas daerah tersebut. apabila kondisi berikut dipenuhi: Untuk setiap bilangan ε > 0 apapun terdapat sebuah bilangan δ > 0 yang berkorespondensi dengannya sedemikian rupanya untuk setiap partisi
apabila kondisi berikut dipenuhi: Untuk setiap bilangan ε > 0 apapun terdapat sebuah bilangan δ > 0 yang berkorespondensi dengannya sedemikian rupanya untuk setiap partisi 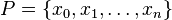 di sepanjang [a,b] dengan
di sepanjang [a,b] dengan 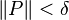 dan pilihan ti apapun pada [xk - 1, ti], kita dapatkan
dan pilihan ti apapun pada [xk - 1, ti], kita dapatkan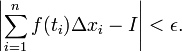
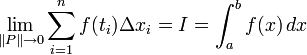

 , yakni mencari luas daerah A dibawah kurva y=x pada interval [0,b], b>0, maka perhitungan integral tertentu
, yakni mencari luas daerah A dibawah kurva y=x pada interval [0,b], b>0, maka perhitungan integral tertentu 
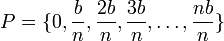 dan
dan  , sehingga:
, sehingga:

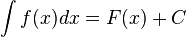
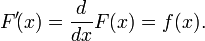

 adalah sebuah bilangan, manakala integral tak tentu :
adalah sebuah bilangan, manakala integral tak tentu :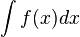 adalah sebuah fungsi yang memiliki tambahan konstanta sembarang C.
adalah sebuah fungsi yang memiliki tambahan konstanta sembarang C.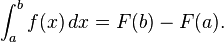
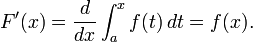
 , daripada menggunakan definisi integral tertentu sebagai limit dari penjumlahan Riemann (
, daripada menggunakan definisi integral tertentu sebagai limit dari penjumlahan Riemann (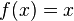 adalah
adalah  . Oleh sebab itu, sesuai dengan teorema dasar kalkulus, nilai dari integral tertentu
. Oleh sebab itu, sesuai dengan teorema dasar kalkulus, nilai dari integral tertentu 







